|
|
 |
The Yahoo Bonus and its Impact on Search Engine
Optimization |
|
|
|
Many experts in search engine optimization
assume that certain websites obtain a special PageRank
evaluation from the Google search engine which needs a manual
intervention and does not derive from the PageRank algorithm
directly. Mostly, the directories Yahoo and Open Directory
Project (dmoz.org) are considered to get this special
treatment. In the context of search engine optimization, this
assumption would have the consequence that an entry into the
above mentioned directories had a big impact on a site's
PageRank.
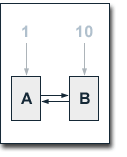 An approach that is often mentioned when talking
about influencing the PageRank of certain websites is to
assign higher starting values to them before the iterative
computation of PageRank begins. Such proceeding shall be
reviewed by looking at a simple example web consisting of two
pages, whereby each of these pages solely links to the other.
We assign an initial PageRank of 10 to one page and a PageRank
of 1 to the other. The damping factor d is set to 0.1, because
the lower d is, the faster the PageRank values converge during
the iterations. So, we get the following equations for the
computation of the pages' PageRank values:
PR(A) = 0.9
+ 0.1 PR(B)
PR(B) = 0.9 + 0.1 PR(A)
During the
iterations, we get the following PageRank values:
| Iteration |
PR (A) |
PR (B) |
| 0 |
1 |
10 |
| 1 |
1.9 |
1.09 |
| 2 |
1.009 |
1.0009 |
| 3 |
1.00009 |
1.000009 |
It is
obvious that despite assigning different starting values to
the two pages each of the PageRank values converges to 1, just
as it would have happened if no initial values were assigned.
Hence, starting values have no effect on PageRank if a
sufficient number of iterations takes place. Indeed, if the
computation is performed with only few iterations, the
starting values would influence PageRank. But in this case, we
have to consider that in our example the PageRank relation
between the two pages reverses after the first iteration.
However, it shall be noted that for our computation the actual
PageRank values within one iteration have been used and not
the ones from the previous iteration. If those values would
have been used, the PageRank relation had alternated after
each iteration.
|
|
|
Modification of the PageRank Algorithm
|
|
|
|
If assigning special starting values at the begin of
the PageRank calculations has no effect on the results of the
computation, this does not mean that it is not possible to
influence the PageRank of websites or web pages by an
intervention in the PageRank algorithm. Lawrence Page, for
instance, describes a method for a special evaluation of web
pages in his PageRank patent specifications (United States
Patent 6,285,999). The starting point for his consideration is
that the random surfer of the Random Surfer Model may get
bored and stop following links with a constant probabilty, but
when he restarts, he won't take a random jump to any page of
the web but will rather jump to certain web pages with a
higher probability than to others. This behaviour is closer to
the behaviour of a real user, who would more likely use, for
instance, directories like Yahoo or ODP as a starting point
for surfing.
If a special evaluation of certain web
pages shall take place, the original PageRank algorithm has to
be modified. With another expected value implemented, the
algorithm is given as follows:
PR(A) = E(A) (1-d) + d
(PR(T1)/C(T1) + ... + PR(Tn)/C(Tn))
Here, (1-d) is the
probability for the random surfer no longer following links.
E(A) is the probability for the random surfer going to page A
after he has stopped following links, weighted by the number
of web pages. So, E is another expected value whose average
over all pages is 1. In this way, the average of the PageRank
values of all pages of the web will continue to converge to 1.
Thus, the PageRank values do not vaccilate because of the
special evaluation of web pages and the impact of PageRank on
the general ranking of web pages remains stable.
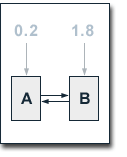 In our example, we set the
probability for the random surfer going to page A after he has
stopped following links to 0.1. The probability for him going
to page B is set to 0.9. Since our web consists of two pages
E(A) equals 0.2 and E(B) equals 1.8. At a damping factor d of
0.5 we get the following equations for the calculation of the
single pages' PageRank values:
PR(A) = 0.2 × 0.5 + 0.5
× PR(B)
PR(B) = 1.8 × 0.5 + 0.5 × PR(A)
If we solve
these equations we get the following PageRank values:
PR(A) = 11/15
PR(B) = 19/15
The sum of the
PageRank values remains 2. The higher probability for the
random surfer jumping to page B is reflected by its higher
PageRank. Indeed, the uniform interlinking between both pages
prevents our example pages' PageRank values from a more
significant impact of our intervention.
So, it is
possible to implement the special evaluation of certain web
pages into the PageRank algorithm without having to change it
fundamentally. It is questionable, indeed, what criteria is
used for the evaluation. Lawrence Page suggests explicitly the
utilization of real usage data in his PageRank patent
specifications. Google, meanwhile, collects usage date by
means of the Google Toolbar. And Google would not even need as
much data, as if the whole ranking was solely based on usage
data. A limited sample would be sufficient to determine the
1,000 or 10,000 most important pages on the web. The PageRank
algorithm can then fill the holes in usage data and is thereby
able to deliver a more accurate picture of the web.
Of
course, all statements regarding the influence of real usage
data on PageRank are pure speculation. Even if there is a
special evaluation of certain web pages at all will in the
end, stay a secret of the people at Google. |
|
|
Nonetheless, Assigning Starting Values?
|
|
|
|
Although, assigning special starting values to pages at
the begin of PageRank calculations has no effect on PageRank
values it can, nonetheless, be reasonable.
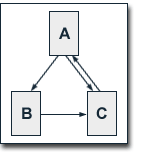 We take a look at our example web
consisting of the pages A, B and C, whereby page A links to
the pages B and C, page B links to page C and page C links to
page A. In this case, the damping factor d is set to 0.75. So,
we get the following equations for the iterative computation
of the single pages' PageRank values:
PR(A) = 0.25 +
0.75 PR(C)
PR(B) = 0.25 + 0.75 (PR(A) / 2)
PR(C) = 0.25
+ 0.75 (PR(A) / 2 + PR(B))
Basically, it is not
necessary to assign starting values to the single pages before
the computation begins. They simply start with a value of 0
and we get the following PageRank values during the
iterations:
|
| Iteration |
PR(A) |
PR(B) |
PR(C) |
| 0 |
0 |
0 |
0 |
| 1 |
0.25 |
0.34375 |
0.60156 |
| 2 |
0.70117 |
0.51294 |
0.89764 |
| 3 |
0.92323 |
0.59621 |
1.04337 |
| 4 |
1.03253 |
0.63720 |
1.11510 |
| 5 |
1.08632 |
0.65737 |
1.15040 |
| 6 |
1.11280 |
0.66730 |
1.16777 |
| 7 |
1.12583 |
0.67219 |
1.17633 |
| 8 |
1.13224 |
0.67459 |
1.18054 |
| 9 |
1.13540 |
0.67578 |
1.18261 |
| 10 |
1.13696 |
0.67636 |
1.18363 |
| 11 |
1.13772 |
0.67665 |
1.18413 |
| 12 |
1.13810 |
0.67679 |
1.18438 |
| 13 |
1.13828 |
0.67686 |
1.18450 |
| 14 |
1.13837 |
0.67689 |
1.18456 |
| 15 |
1.13842 |
0.67691 |
1.18459 |
| 16 |
1.13844 |
0.67692 |
1.18460 |
| 17 |
1.13845 |
0.67692 |
1.18461 |
| 18 |
1.13846 |
0.67692 |
1.18461 |
| 19 |
1.13846 |
0.67692 |
1.18461 |
| 20 |
1.13846 |
0.67692 |
1.18461 |
| 21 |
1.13846 |
0.67692 |
1.18461 |
| 22 |
1.13846 |
0.67692 |
1.18462 |
If
we assign 1 to each page before the computation starts, we get
the following PageRank values during the iterations:
| Iteration |
PR(A) |
PR(B) |
PR(C) |
| 0 |
1 |
1 |
1 |
| 1 |
1 |
0.625 |
1.09375 |
| 2 |
1.07031 |
0.65137 |
1.13989 |
| 3 |
1.10492 |
0.66434 |
1.16260 |
| 4 |
1.12195 |
0.67073 |
1.17378 |
| 5 |
1.13034 |
0.67388 |
1.17928 |
| 6 |
1.13446 |
0.67542 |
1.18199 |
| 7 |
1.13649 |
0.67618 |
1.18332 |
| 8 |
1.13749 |
0.67656 |
1.18398 |
| 9 |
1.13798 |
0.67674 |
1.18430 |
| 10 |
1.13823 |
0.67684 |
1.18446 |
| 11 |
1.13835 |
0.67688 |
1.18454 |
| 12 |
1.13840 |
0.67690 |
1.18458 |
| 13 |
1.13843 |
0.67691 |
1.18460 |
| 14 |
1.13845 |
0.67692 |
1.18461 |
| 15 |
1.13845 |
0.67692 |
1.18461 |
| 16 |
1.13846 |
0.67692 |
1.18461 |
| 17 |
1.13846 |
0.67692 |
1.18461 |
| 18 |
1.13846 |
0.67692 |
1.18461 |
| 19 |
1.13846 |
0.67692 |
1.18462 |
If we
now assign a starting value to each page, which is closer to
its effective PageRank (1.1 for page A, 0.7 for page B and 1.2
for page C), we get the following results:
| Iteration |
PR(A) |
PR(B) |
PR(C) |
| 0 |
1.1 |
0.7 |
1.2 |
| 1 |
1.15 |
0.68125 |
1.19219 |
| 2 |
1.14414 |
0.67905 |
1.18834 |
| 3 |
1.14126 |
0.67797 |
1.18645 |
| 4 |
1.13984 |
0.67744 |
1.18552 |
| 5 |
1.13914 |
0.67718 |
1.18506 |
| 6 |
1.13879 |
0.67705 |
1.18483 |
| 7 |
1.13863 |
0.67698 |
1.18472 |
| 8 |
1.13854 |
0.67695 |
1.18467 |
| 9 |
1.13850 |
0.67694 |
1.18464 |
| 10 |
1.13848 |
0.67693 |
1.18463 |
| 11 |
1.13847 |
0.67693 |
1.18462 |
| 12 |
1.13847 |
0.67692 |
1.18462 |
| 13 |
1.13846 |
0.67692 |
1.18462 |
So, the
closer the assigned starting values are to the effective
results we would get by solving the equations, the faster do
the PageRank values converge in the iterative computation.
Less iterations are needed, which can be useful for providing
more up to date search results, especially regarding the
growth rate of the web. Starting point for an accurate
presumption of the actual PageRank distribution ay be the
PageRank values of a former PageRank calculation. All the
pages which are new in the imndex could get an initial PageRank
of 1, which will then be a lot closer to the effective
PageRank value after the first few iterations. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PageRank and Google are trademarks of Google Inc.,
Mountain View CA, USA.
PageRank is protected by US Patent
6,285,999.
The content of this document may be
reproduced on the web provided that a copyright notice is
included and that there is a straight HTML hyperlink to the
corresponding page at pr.efactory.de in direct
context. |
|
|
|
| |
|
