|
|
 |
The Effect of Inbound Links |
 |
|
 |
It has already been shown that each
additional inbound link for a web page always increases that
page's PageRank. Taking a look at the PageRank algorithm,
which is given by
PR(A) = (1-d) + d (PR(T1)/C(T1) +
... + PR(Tn)/C(Tn))
one may assume that an additional
inbound link from page X increases the PageRank of page A by
d × PR(X) / C(X)
where PR(X) is the PageRank
of page X and C(X) is the total number of its outbound links.
But page A usually links to other pages itself. Thus, these
pages get a PageRank benefit also. If these pages link back to
page A, page A will have an even higher PageRank benefit from
its additional inbound link.
The single effects of
additional inbound links shall be illustrated by an example.
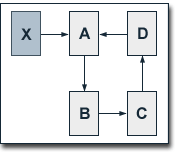 We regard a website consisting of four pages A, B, C
and D which are linked to each other in circle. Without
external inbound links to one of these pages, each of them
obviously has a PageRank of 1. We now add a page X to our
example, for which we presume a constant Pagerank PR(X) of 10.
Further, page X links to page A by its only outbound link.
Setting the damping factor d to 0.5, we get the following
equations for the PageRank values of the single pages of our
site: We regard a website consisting of four pages A, B, C
and D which are linked to each other in circle. Without
external inbound links to one of these pages, each of them
obviously has a PageRank of 1. We now add a page X to our
example, for which we presume a constant Pagerank PR(X) of 10.
Further, page X links to page A by its only outbound link.
Setting the damping factor d to 0.5, we get the following
equations for the PageRank values of the single pages of our
site:
PR(A) = 0.5 + 0.5 (PR(X) + PR(D)) = 5.5 + 0.5
PR(D)
PR(B) = 0.5 + 0.5 PR(A)
PR(C) = 0.5 + 0.5
PR(B)
PR(D) = 0.5 + 0.5 PR(C)
Since the total
number of outbound links for each page is one, the outbound
links do not need to be considered in the equations. Solving
them gives us the following PageRank values:
PR(A) =
19/3 = 6.33
PR(B) = 11/3 = 3.67
PR(C) = 7/3 =
2.33
PR(D) = 5/3 = 1.67
We see that the initial
effect of the additional inbound link of page A, which was
given by
d × PR(X) / C(X) = 0,5 × 10 / 1 = 5
is passed on by the links on our site. |
|
|
The Influence of the Damping Factor
|
|
|
|
The degree of PageRank propagation from one page to
another by a link is primarily determined by the damping
factor d. If we set d to 0.75 we get the following equations
for our above example:
PR(A) = 0.25 + 0.75 (PR(X) +
PR(D)) = 7.75 + 0.75 PR(D)
PR(B) = 0.25 + 0.75
PR(A)
PR(C) = 0.25 + 0.75 PR(B)
PR(D) = 0.25 + 0.75
PR(C)
Solving these equations gives us the following
PageRank values:
PR(A) = 419/35 = 11.97
PR(B) =
323/35 = 9.23
PR(C) = 251/35 = 7.17
PR(D) = 197/35 =
5.63
First of all, we see that there is a
significantly higher initial effect of additional inbound link
for page A which is given by
d × PR(X) / C(X) = 0.75 ×
10 / 1 = 7.5
This initial effect is then propagated
even stronger by the links on our site. In this way, the
PageRank of page A is almost twice as high at a damping factor
of 0.75 than it is at a damping factor of 0.5. At a damping
factor of 0.5 the PageRank of page A is almost four times
superior to the PageRank of page D, while at a damping factor
of 0.75 it is only a little more than twice as high. So, the
higher the damping factor, the larger is the effect of an
additional inbound link for the PageRank of the page that
receives the link and the more evenly distributes PageRank
over the other pages of a site. |
|
|
The Actual Effect of Additional Inbound
Links
|
|
|
|
At a damping factor of 0.5, the accumulated PageRank of
all pages of our site is given by
PR(A) + PR(B) +
PR(C) + PR(D) = 14
Hence, by a page with a PageRank of
10 linking to one page of our example site by its only
outbound link, the accumulated PageRank of all pages of the
site is increased by 10. (Before adding the link, each page
has had a PageRank of 1.) At a damping factor of 0.75 the
accumulated PageRank of all pages of the site is given by
PR(A) + PR(B) + PR(C) + PR(D) = 34
This time
the accumulated PageRank increases by 30. The accumulated
PageRank of all pages of a site always increases by
(d
/ (1-d)) × (PR(X) / C(X))
where X is a page
additionally linking to one page of the site, PR(X) is its
PageRank and C(X) its number of outbound links. The formula
presented above is only valid, if the additional link points
to a page within a closed system of pages, as, for instance, a
website without outbound links to other sites. As far as the
website has links pointing to external pages, the surplus for
the site itself diminishes accordingly, because a part of the
additional PageRank is propagated to external pages.
The justification of the above formula is given by
Raph Levien and it is based on the Random Surfer Model. The
walk length of the random surfer is an exponential
distribution with a mean of (d/(1-d)). When the random surfer
follows a link to a closed system of web pages, he visits on
average (d/(1-d)) pages within that closed system. So, this
much more PageRank of the linking page - weighted by the
number of its outbound links - is distributed to the closed
system.
For the actual PageRank calculations at
Google, Lawrence Page und Sergey Brin claim to usually set the
damping factor d to 0.85. Thereby, the boost for a closed
system of web pages by an additional link from page X is given
by
(0.85 / 0.15) × (PR(X) / C(X)) = 5.67 × (PR(X) /
C(X))
So, inbound links have a far larger effect than
one may assume. |
|
|
The PageRank-1 Rule
|
|
|
|
Users of the Google Toolbar often notice that pages
with a certain Toolbar PageRank have an inbound link from a
page with a Toolbar PageRank which is higher by one. Some take
this observation to doubt the validity of the PageRank
algorithm presented here for the actual ranking methods of the
Google search engine. It shall be shown, however, that the
PageRank-1 rule complies with the PageRank algorithm.
Basically, the PageRank-1 rule proves the fundamental
principle of PageRank. Web pages are important themselves if
other important web pages link to them. It is not necessary
for a page to have many inbound links to rank well. A single
link from a high ranking page is sufficient.
To show
the actual consistance of the PageRank-1 rule with the
PageRank algorithm several factors have to be taken into
consideration. First of all, the toolbar PageRank is a
logarithmically scaled version of real PageRank values. If the
PageRank value of one page is one higher than the PageRank
value of another page in terms of Toolbar PageRank, than its
real PageRank can at least be higher by an amount which equals
the logarithmical basis for the scalation of Toolbar PageRank.
If the logarithmical basis for the scalation is 6 and the
toolbar PageRank of a linking Page is 5, then the real
PageRank of the page which receives the link can be at least 6
times smaller to make that page still get a toolbar PageRank
of 4.
However, the number of outbound links on the
linking page thwarts the effect of the logarithmical basis,
because the PageRank propagation from one page to another is
devided by the number of outbound links on the linking page.
But it has already been shown that the PageRank benefit by a
link is higher than PageRank algorithm's term d(PR(Ti)/C(Ti))
pretends. The reason is that the PageRank benefit for one page
is further distributed to other pages within the site. If
those pages link back as it usualy happens, the PageRank
benefit for the page which initially received the link is
accordingly higher. If we assume that at a high damping factor
the logarithmical basis for PageRank scalation is 6 and a page
receives a PageRank benefit which is twice as high as the
PageRank of the linking page devided by the number of its
outbound links, the linking page could have at least 12
outbound links so that the Toolbar PageRank of the page
receiving the link is still at most one lower than the toolbar
PageRank of the linking page.
A number of 12 outbound
links admittedly seems relatively small. But normally, if a
page has an external inbound link, this is not the only one
for that page. Most likely other pages link to that page and
propagate PageRank to it. And if there are examples where a
page receives a single link from another page and the
PageRanks of both pages comply the PageRank-1 rule although
the linking page has many outbound links, this is first of all
an indication for the linking page's toolbar PageRank being at
the upper end of its scale. The linking page could be a "high"
5 and the page receiving the link could be a "low" 4. In this
way, the linking page could have up to 72 outbound links. This
number rises accordingly if we assume a higher logarithmical
basis for the scalation of Toolbar PageRank. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PageRank and Google are trademarks of Google Inc.,
Mountain View CA, USA.
PageRank is protected by US Patent
6,285,999.
The content of this document may be
reproduced on the web provided that a copyright notice is
included and that there is a straight HTML hyperlink to the
corresponding page at pr.efactory.de in direct
context. |
|
|
|
| |
|